OnDeck Capital is one of the most popular daily debit business loan products. The OnDeck APR Calculator not only works for OnDeck but also most of the daily debit, cashflow based loan products. It’s a good tool to figure out the APR and make an apple-to-apple comparison with a merchant cash advance or a term loan.

First, I would like to mention that the APR we calculate here is not 100% precise. But it’s very close. The reason is that most of the daily debit loans only debit on business days, not weekend days. If you get funded on a Friday, you don’t start paying until two days later (Monday). But if you get funded on a Monday, you have to start paying the next day. This will result in slightly different APRs with the former scenario having a higher APR. We think the APR difference is small enough to NOT take into account the day of the week a loan is funded. Instead, we calculate the APR the following way:

Instead of asking you on which day of the week you are being funded, we assume you are making 7 equal payments per week on each day (vs. paying $X on Mondays to Fridays and $0 on Saturdays and Sundays).

• New Number of Payments is equal to (Number of Payments)/57
• New Daily Payment is equal to (Payback Amount)/(New Number of Payments)
• Daily Rate is equal to the result of the excel formula of =RATE(New Number of Payments, New Daily Payment, -(Loan Amount – Origination Fee))
• APR is equal to (Daily Rate) 365. We are using daily compounding and assume there’re 365 days in a year.

Averaging out 5 weekday payments to 7 days gives a pretty accurate estimate of the loan APR. In most cases, you wouldn’t know which day you are going to get funded when you apply, this estimate gives you a very precise average and helps you compare across different products like a term loan or a merchant cash advance.

You’re 3X more likely to get approved for a business credit card with MatchFactor.

Instantly see your top options for business loans and credit cards based on your business needs using Nav's MatchFactor.

Get matched

A 30% Term Loan vs. A 20% OnDeck Loan

When you get a loan offer from OnDeck, on the term sheet it will tell you the interest rate is 20%. But that’s not the annualized interest rate. It’s 20% of the principal. On the other hand, a bank loan or a loan from LendingClub or FundingCircle, the quoted interest rates are the annualized interest rate, which is the same type of interest rate quote you get from a mortgage loan. It’s quite confusing to compare between the two different types of interest rates. That’s why it’s important to bring everything into the same APR basis so apple-to-apple comparisons can be made.

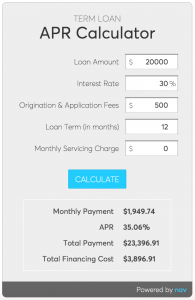
Let’s compare two $20,000 loans A and B, both with a 2.5% origination fee. Loan A has an annualized interest rate of 30% with 12-month amortization while Loan B has a 20% interest rate based on loan principal with 125 equal weekday payments (25 weeks). Pictures are worth 1000 words. You can see the APR and Total Cost comparison below.

A	B

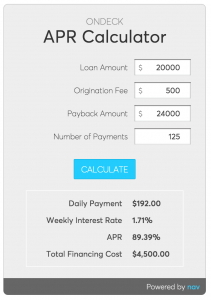As you can see, the 30% term loan has a lower total cost ($3,897), longer payback period (12 months) while the 20% OnDeck/Daily Debit loan has a higher total cost ($4,500), shorter payback period (~6 months). If you are qualified for both, there’s no reason to take the latter option because the 30% term loan is cheaper and has a lower monthly payment.

The above example is the main motivation why we create the Nav calculators. Before you commit to a loan, shop around and compare offers with our calculators. Find the best option and use the saved cash to grow your business.

Have you seen Business Manager?

Full business credit reports & scores from Dun & Bradstreet, Experian and Equifax.

Get started today